Stefano Rossignoli – 9 novembre 2016
…23 anni fa oggi partivo per militare, uscito dalle superiori con “tre meno meno meno” in matematica, un calcio nel sedere, il minimo dei voti e giurando a me stesso che non avrei mai più studiato in una scuola…ed ora ecco qui lo Ste che, fortunatamente, ha rotto qualche tempo fa quello stupido giuramento…
Ma torniamo a noi…
Innanzi a tutto è un piacere tornare a scrivere su scienzafacile.it dopo così tanto tempo…
La mia preparazione di base nelle materie scientifiche, mescolati ad una carissima amica e un centro specializzato, mi hanno portato a trovarmi coinvolto come tutor a ragazzi con DSA.
Se volete saperne di più sul DSA (ovvero i disturbi specifici dell’apprendimento), cliccate su questo link: http://www.disturbiapprendimento.com/.
E’ un lavoro che mi occupa parecchio tempo, anche quando apparentemente non lavoro e che comunque tengo strettamente privato e ne parlo solo vagamente per tutelare i miei “tutorati”.
Avendo però ogni tanto qualche idea che funziona, ho deciso che, almeno quelle che OGGETTIVAMENTE funzionano, le pubblicherò qui, tempo permettendo. Questo è uno dei vari motivi per cui vorrei leggere e fornire di files audio tutti gli articoli del sito…anche se magari non ce la farò mai…
L’articolo è rivolto alle e agli insegnanti ma, perchè no, anche a chi con dsa o qualche dubbio sull’argomento, voglia sbatterci un po’ la testa da sola o da solo!
Il maggiore e il minore sono spesso ostacoli enormi per chi soffre in forma grave di disturbi specifici dell’apprendimento.
In questo periodo sto affrontando questo argomento con uno dei “miei” ragazzi ma NON dal punto di vista elementare.
In effetti, da questo punto di vista, è facile insegnare a riconoscere il simbolo “>” dal simbolo “<” ed è facile anche che i bambini ne comprendano presto il significato e imparino ad usarlo autonomamente.
Per questo, anche su internet, con una semplice ricerca, si trovano buoni suggerimenti per aggirare questo ostacolo…
Il muro duro da abbattere l’ho trovato quando ci siamo “scontrati” con una disequazione, una disequazione fratta o a un sistema di disequazioni…non tanto nel metodo di risoluzione che è complesso ma strutturabile in modo quasi sempre ordinato, quanto nella traduzione del grafico risolutivo.
Come scrivo la soluzione? Sembrerà banale per chi non ha di questi problemi ma, a volte, non lo è per nulla, ve lo assicuro!
Il mio lavoro è quello di “hakerare” il problema, ovvero di aggirarlo, utilizzando il bagaglio già acquisito del ragazzo, in modo da fargli apprendere e maneggiare il nuovo concetto o il nuovo meccanismo.
Per questo ho “inventato” , ma forse no, questo metodo che chiamerò “Metodo della x” per cui vi invito a leggere un P.S. in fondo all’articolo.
La lettera “x” è formata da un maggiore e da un minore come vediamo in figura:

Mi avvalgo di una semplice disequazione fratta di esempio per spiegare il metodo che ho insegnato per scrivere la soluzione della disequazione:
Prima di tutto le condizioni di esistenza…!!! E’ vero che nelle disequazioni fratte non sono così necessarie ma quando la x è al denominatore a me piace comunque iniziare con le C.E….
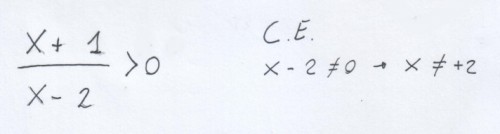
Poi studiamo il segno mettendo il numeratore maggiore di zero (qui non è necessario l’uguale perché non è richiesto nel testo dell’operazione!)
e il denominatore maggiore di zero (questo invece non va mai uguale a zero visto che non si può dividere per zero…e questo dovremmo saperlo tutte e tutti e, per questo motivo le C.E. non sono così necessarie!)

Realizzo il grafico dello studio del segno e guardo quando quest’ultimo è maggiore di zero come richiesto dalla disequazione, il che rappresenterà la soluzione…
Fino a qui nessun problema con quello che un alunno dovrebbe saper fare in seconda o terza superiore…poi…
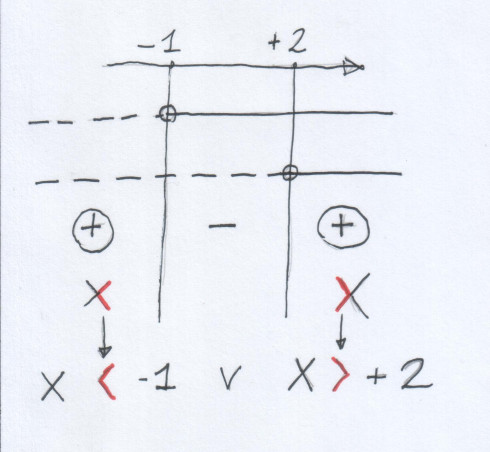
…per scrivere la soluzione, ovvero l’ultima riga dell’esempio, si vede come prendo la metà della x rivolta verso il numero a cui devo rapportarla e questo è quanto!!!
Ognuno ha i suoi skills (perdonate ma non mi viene in italiano!) e ognuno i suoi bug. Ed è tutto estremamente affascinante da studiare e cercare di risolvere!
Il metodo è valido anche per valori di x compresi tra due numeri, con la differenza che la soluzione verrà scritta in modo un po’ strano come per esempio x > -1 e x < +2 invece di -1 < x < +2 …ma, insegnare a scrivere questo tipo di soluzione a me è risultato molto più facile che non il precedente…che (bando alle ciance e alle persone fiscali) è sempre valido!!!
E così via per sistemi di disequazioni, eccetra, eccetra…!
Grazie di avermi letto!
Mi do io stesso il bentornato su scienzafacile.it e, a presto!
Stefano!
P.S.
Il “metodo della x” non credo di averlo inventato. E’ troppo ovvio per non essere già stato utilizzato…
Credo che i simboli maggiore e minore derivino proprio dalla forma della x o anche, e più probabile, che la x sia stata scelta come variabile di base proprio perché è formata da un maggiore e da un minore.
Semplicemente, forse, su internet non si trovano notizie o “forse” si tende a non insegnare concetti considerati troppo complicati e questo invece è il bello della sfida. Poi, che ognuno/a abbia bisogno o arrivi ad utilizzare metodi totalmente personali e unici, è un aspetto che rende il tutto ancor più affascinante …indubbiamente faticoso!!!
Purtroppo la mia ignoranza non mi permette di trovare una fonte attendibile per questa mia ipotesi…
